Third Trilateral Meeting “Australia -Taiwan - Italia”

We study the problem of minimizing

Curvature-driven surface diffusion on crystalline surfaces is modeled bythe nonlinear 4th order Mullins equation. There is a class of weaklyanisotropic nonlinear models that is fully integrable. Exact solutions areconstructed for development of a grain boundary groove and for smoothing ofan initial ramp dislocation. For the grooving problem, a piecewisenonlinear but solvable model can be made arbitrarily close to the isotropicnonlinear Mullins equation. The solution shows that unlike in the linearmodel, the groove depth remains bounded as the dihedral angle approachesvertical. At a dislocation point of infinite curvature, the quasilinearMullins model should be extended to a fully nonlinear model to account forGibbs-Thompson

I will discuss some aspects of recent research on the analytic approach tospectral flow for unbounded self adjoint Fredholm operators.

We present some general uniqueness results dealing with positive solutionsof

such that lim _{d(x) → 0} u(x) =∞, where Ω is a smooth boundeddomain in R^N and d(x) := dist(x, ∂Ω). We assume that b is a continuous nonnegative function on the closureof Ω, a is a realnumber and f is locally Lipschitz continuous on[0, ∞) with f(u)/u increasing for u > 0. We analysethe competing case when b(x) vanishes on ∂Ω at a regular rate (e.g., [d(x)]^α with α > 0) or rapid rate (e.g., exp(-[d(x)]^q) with q <0), while f varies regularly at ∞ with index p > 1(that is lim_{u → ∞}f(λu)/f(u)= λ^p, for every λ >0). The extreme case when p = ∞ willalso be considered. We emphasize the links between the asymptotic behaviourof the blow-up solution and the variation speeds of f and b.

We discuss finite Morse index solutions of supercritical ellipic problemson unbounded domains and their application to supercritical problems onbounded domains.

The two geometric flows in the title are the gradient flows associated tocertain energy functionals. In the considered dimension, (i.e. dimension 2for the harmonic map heat flow, dimension 4 for the Yang Mills heat flow),the associated energy functional is (locally) conformally invariant, i.e.the dimension is critical. In this talk we discuss similarities anddifferences between the flows in certain symmetric situations.

We consider the weak continuity of the 2-Hessian operator on non-commutingvector fields satisfying the Hormander condition.

When the wave speed is zero in a bistable system, there is a naturalvariational setting for the problem of finding a travelling wave. If thewave speed is not zero, it is difficult to use variational method to find asolution. In this talk, we are going to discuss the possible variationalstructure for the case with non-zero wave speed.

The purpose of this paper is to study thememory (or nonlocal) effect induced by homogenization of theMaxwell equations. The memory kernel is described by the Volterraintegral equation. Furthermore, it can be characterized explicitlyin terms of Young's measure, and the kinetic formulation of thehomogenized equation is also obtained. The kinetic formulationallows us to obtain the homogenization of the energy density andthe associated conservation law with the Poynting vector. Theinteresting interaction phenomenon of the microscopic andmacroscopic scales is also discussed and the memory effectexplains qualitatively something about irreversibility.

The Marcinkiewicz integral defined by

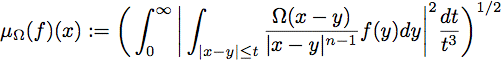
is essentially a Littlewood-Paley g-function,which plays a very important role in harmonic analysis. In the talk, wefirst survey the L^p boundedness andweighted L^p boundedness of theMarcinkiewicz integral, and then introduce other recent results concerningthe Marcinkiewicz integral with rough kernel and its new development.

In this paper we prove three spheres inequalities for a two-dimensionalstrongly elliptic system. We then give an application of these threespheres inequalities to the inverse problem of identifying cavities bypartial boundary measurements.

Here we study the ground state solution of a coupled system of nonlinearSchrodinger equations with external trap potentials. The coupled system isa model which describes a binary mixture of Bose-Einstein condensates. Dueto Feshbach resonance, the coupled system can be transformed into asingular perturbed problem with a small parameter. As the parameter goes tozero, the existence and the asymptotic behavior of ground state solutionscan be proved, and spikes can be found in these ground state solutions.Furthermore, we may figure out how trap potentials affect the locations andconfigurations of spikes.

Multi-dimensional Euler equations in gas dynamics possess very rich andcomplex wave phenomena. There are definite experimental and computationalresults, but preciously little analytical understanding. In fact, to theembarassments of the workers in the field, the classical book ofCourant-Friedrichs “Supersonic Flows and Shock Waves ”, writtenin 1948, is still mostly updated. Due to the obvious difficulties of thepresence of shock waves, one of the main efforts to identify physicallyimportant problems that have simple scaling properties. Two such problemshave already reported in Courant-Friedrichs. One is to find the criterionof the transition of the regular-Mach shock reflections for a shock wavemoving toward a ramp. The other is the determination of the phsicality ofthe weak-strong shock reflections for supersonic flows around a wedge. Wewill formulate these problems and report on the recent progresses on them.For these problems, the scaling analysis reduces the dimensions and theflows become self-similar. This simplifies the problem. On the other hands,the equations in self-smilarity coordinates are of mixed types, even thoughthe original Euler equations are hyperbolic. To avoid the issue of highlyunstable vortex sheets and to concentrate on the study of shock andacoustic waves, one considers the potential equations. In self-similarcoordinates, there are interesting goemetric consequences, such as thebasic Ellipticity Principle. The question of well-posedness of boundaryvalue problem for degenerate elliptic equation with the free boundary ofshock waves and degenerate sonic circles is also very interesting. Newissues arise for elliptic PDEs.

There are several fundamental singular limit problems such as the zerodissipation limits for coservation laws and the zero mean free path limitfor Boltzmann equation. The limits are singular because of the presence ofinitial, boundary and shock layers. We plan to discuss the recent analysisin dealing with some of these limits.

The p-laplacian operator and its non standardversion, the p(x)-laplacian, have been the objectof an intensive study in the last years. In particular, several regularityresults have been obtained, concerning the integrability properties ofsolutions both in the elliptic and parabolic cases.

This talk will illustrate some recent results obtained in collaborationwith G. Mingione, the newest of which are two Calderón-Zygmundtype theorems, covering the following statement, where the exponent p may be even below 2: IfF is in L^q_loc for some q > p then the solutions uof the parabolic system of PDEs

are such that Du belongs to L^q_loc.

The technique employed contains some fundamental elements derived from asimilar theory developed for the elliptic p(x)-laplacian.

We survey some recent results on NLS. Some new trends on this field willalso be discussed.

In this talk we describe a recent joint work with W.Gangbo. We consider aHamiltonian H on P₂(R^2d), the set of probabilitymeasures with finite quadratic moments on the phase space R^2d, which is ametric space when endowed with the Wasserstein distance W₂. We study the initial value problem dμ_t/dt + ∇ (J_d v_tμ_t) = 0, where J_dis the canonical symplectic matrix, μ₀ is prescribed, v_t is a tangent vector to P₂(R^2d) at μ_t, and belongs to ∂H(μ^t), the subdifferential ofH at &mu_t.

Concerning existence of solutions, two methods for constructing solutionsof the evolutive system are provided. The first one concerns only the casewhere μ₀ is absolutely continuous.It ensures that μ_t remainsabsolutely continuous and v_t = ∇H(μ_t) is the element of minimal norm in ∂ H(μ_t). The second method handlesany initial measure μ₀. If wefurthermore assume that H is λ-convex, proper and lower semicontinuous onP₂(R^2d), we prove that the Hamiltonianis preserved along any solution of our evolutive system.

Concerning uniqueness of solutions, the problem is still largely open andrecent progress on “generic” uniqueness results in thefinite-dimensional case will be described.

We consider the “gauge theory” functional

where A = i &Sigma A_j dx^jis a connection form with values in u(1)=iR and W is asuperquadratic function which satisfies suitable assumptions.

For physical reasons, we assume N=4 and that themetric < ^. ,^. > isthe Minkowsky metric. A vortex is a critical point of the above functionalstationary in time and with cylindrical symmetry.

In this seminar we will discuss the problems related to the study of theabove functional and we will sketch the proof of the existence of vortices.

The attainable set at time T, from a given closedset of a Euclidean space, is a well known object in control theory. Here,such a set is investigated for the symmetric system

where u(t) takes its values in the closed unitball. A recent result obtained in collaboration with H. Frankowskaguarantees that, for f(x) smooth andnondegenerate, the attainable set at time T >0 satisfies a uniform interior sphere condition. As a consequence ofthis property, the attainable set has finite perimeter. Such an informationwill be further analyzed following the approach of a joint work with P.Cardaliaguet where estimates for the perimeter and volume growth ofattainable sets have recently been obtained.

We present the following result, obtained in collaboration with J. Hounie:a bouded Reinhard domain of Cⁿ⁺¹ withconstant Gauss-Levi curvature and with rotational symmetry in twocomplemantary sets of variables is a ball.

We describe various singular limits for hyperbolic problems related to theincompressible 3-D Navier-Stokes equation. We are going to providehyperbolic approximations for the weak solutions in the class of Leray. Thelimiting properties are deduced by the use of dispersive estimates ofStrichartz type combined with nonlinear waves interaction estimates for thebilinear terms. These approximations are motivated by considerations fromphysics and numerical analysis, in particular there are relations with twoimportant methods. The former is an hyperbolic version the so called ÒquasicompressibilityÓ method investigated for instance by J.L. Lions, Temam andrecently by Nochetto, the latter is a time relaxation limit of diffusivetype related to old numerical results by Garabedian and Chorin. Theseresults have been obtained in collaboration with D. Donatelli.

We discuss existence, nonexistence and stability results for solutions ofsemilinear elliptic equations involving exponential nonlinearities. Moreprecisely, we will deal with the equation

with μ a bounded Radon measure, givingconditions on the measure in order to have existence of solutions. The maintools will be a sharp estimate on solutions of linear elliptic equationswith data in Morrey spaces and a decomposition result for Radon measureswith respect to the Hausdorff measure. We will also deal with the equation

with a boundedness assumption in a Morrey space on the sequence e^u_n, proving aconcentration-compactness result of Brezis-Merle type.